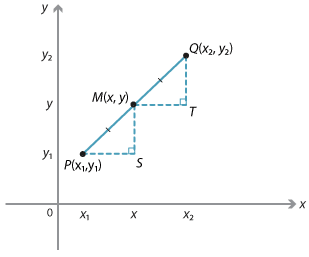![]()
General case
We can find a formula for the midpoint of any interval. Suppose that \(P(x_1, y_1)\) and \(Q(x_2, y_2)\) are two points and let \(M(x, y)\) be the midpoint.
Triangles PMS and MQT are congruent triangles (AAS),
and so \(PS = MT\) and \(MS = QT\).
Hence the x-coordinate of M is the average of \(x_1\) and \(x_2\), and the y-coordinate of M is the average of \(y_1\) and \(y_2\). Therefore:
\(x = \dfrac{x_1 + x_2}{2} \text{and}\ y = \dfrac{y_1 + y_2}{2}\).